Data AnalysisModel

K-Means Clustering(2)

, , ,

개요

  • 이전 포스팅에 이어 Big Query ML에서 K-Means Clustering에서 k값을 결정하는 방법을 알아보자
  • 이 포스팅 하단부에 대한 설명

Elbow Method

  1. 사용하고자 하는 클러스터 범위를 지정한다.

  2. 각 클러스터를 WCSS방법으로 계산을 합니다.

  3. WCSS값과 클러스터 K 갯수에 대한 커브선을 그립니다.

  4. 뾰족하게 구부러진 부분이나 특정 지점이 팔처럼 굽어지는 부분을 K로 지정합니다.

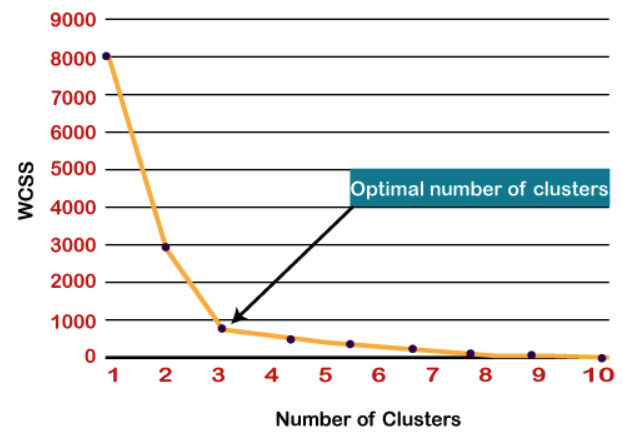
**Within Cluster Sum of Squares(**WCSS)

  • 클러스터 내 제곱합(WCSS)
  • 클러스터 내 모든 포인트에서 클러스터 중심까지의 제곱 평균 거리를 측정
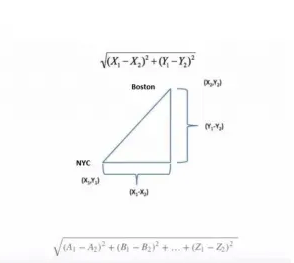
  1. WCSS를 계산하려면 먼저 지정된 포인트와 해당 포인트가 할당된 중심 사이의 유클리드 거리(아래 그림 참조)를 찾는다
  2. 클러스터의 모든 포인트에 대해 이 프로세스를 반복한 다음 클러스터의 값을 합산하고 포인트 수로 나눈다.
  3. 마지막으로 모든 클러스터의 평균을 계산합니다. 이렇게 하면 평균 WCSS가 계산됩니다.

Davies Bouldin Index(DBI)

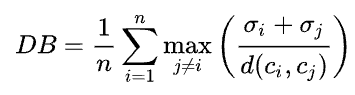
  • n = cluster 개수

  • $c_x$ = cluster $x$의 중심점

  • $\sigma_x$ = cluster $x$내의 모든 데이터 오브젝트로 부터 중심점 $c_x$까지 거리의 평균값

  • $d(c_i,c_j)$ = 중심점 $c_i$와 중심점 $c_j$간의 거리

  • 높은 클러스터 내 유사도를 가지고 낮은 클러스터간 유사도를 가지는 클러스터를 생성하는 클러스터링 알고리즘은 낮은 DBI값을 갖게 됨.

  • 이 지표가 낮은 클러스터링 알고리즘이 좋은 클러스터링 알고리즘으로 평가 됨

  • 간단한 예제를 통해 이해해 보자

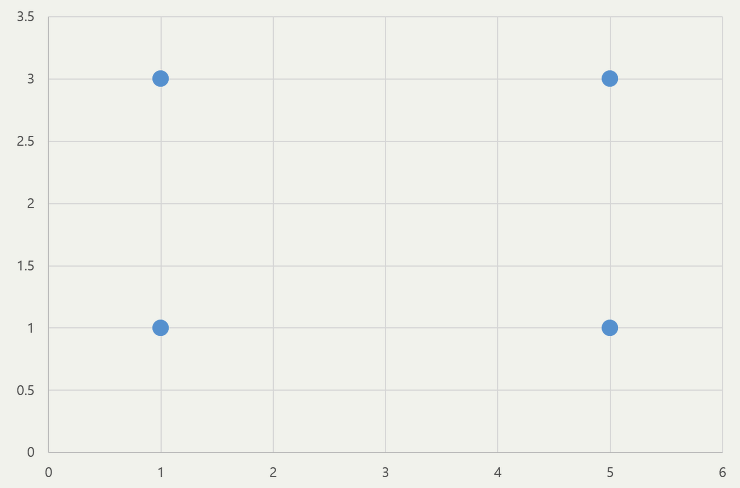
    • 다음과 같이 점 4개가 주어지고 점(1,1)과 점 (1,3)을 중심으로 할때 → 각 그룹의 중심은 (1,3)과 (3,3)으로 나타낼 수 있음.

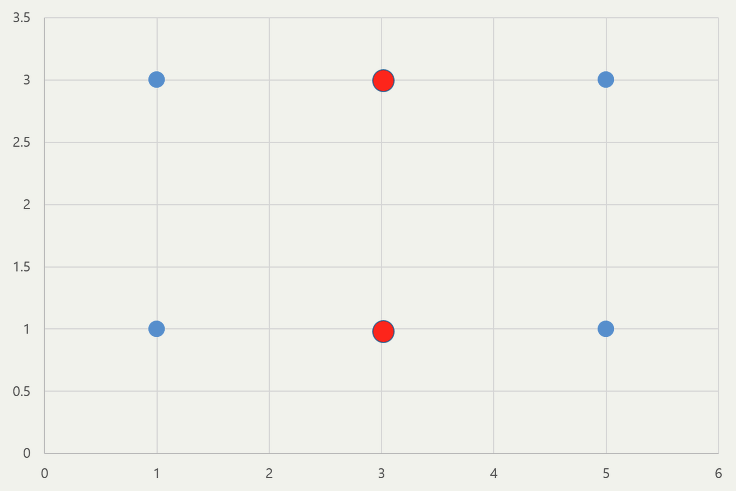
    • 반면 점 (1,1)과 점(1,5)가 중심이 되었을 때 → 각 그룹의 중심은 (1,2)와 (5,2)로 나타남

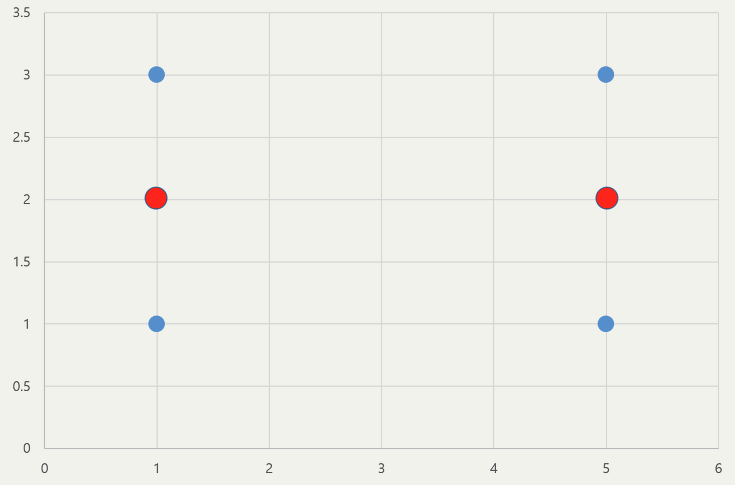
    • 위에서 구한 두 가지 경우들에 대해 각각 DBI값을 구한다면
      • 그룹의 중심이 (1,3)과 (3,3)인 경우: 2
      • 그룹의 중심이 (1,2)와 (5,2)인 경우: 0.5
    • 이 결과를 보았을때 값이 작은 후자의 경우가 cluster를 자세하 구분했다고 말할 수 있음.
Share