Quant

Quant Algorithms_Black Scholes Equation

Black Scholes model explanation

  • 가정: “장난감 가게에서 약속을 사고파는 계산기“라고 생각해봐요. 만약 네가 친구에게 “6개월 뒤에 이 로봇장난감을 10,000원에 살게 약속해줘!”라고 말한다면, 이 약속의 가격을 어떻게 정할까요? 블랙-숄즈 모델은 바로 이 약속값을 계산하는 특별한 계산기예요.
  1. 장난감 현재 가격: 지금 로봇장난감이 10,000원이에요. (S)
  2. 약속 가격: 6개월 뒤에 11,000원에 사기로 했어요. (K)
  3. 시간 요소: 약속 기간이 길수록 값이 비싸져요. 1년 약속 > 1개월 약속 (T)
  4. 장난감 가격 변동: 로봇장난감 가격이 요즘 자주 오르내리면 약속값이 올라요. (σ)
  5. 안전 저금통: 은행에 돈을 맡기면 조금씩 늘어나죠? 그 증가율도 계산에 들어가요. (r)

  • 실제 예시

    상황 계산 결과
    로봇 가격이 오를때 약속값 UP
    로봇 가격이 안변할때 약속값 DOWN
    약속 기간이 1년 → 2년 약속값 UP
    1. d1 계산: (로그(현재가격/약속가격) + (안전이자율 + 변동성²/2)*시간) / (*변동성√시간)
    2. d2 계산: d1 - 변동성 *√시간
    3. 최종 가격: 현재가격N(d1) - 약속가격할인율*N(d2) (여기서 N()은 표준 정규 분포)
    • d1, d2: 옵션 가격 계산의 핵심 변수로, 위험 조정된 확률값

      • d1의 역할

        • 델타(Δ) 계산: N(d1)N(d1)은 콜옵션 1개를 헤지하기 위해 필요한 주식 수17
        • 현재가 대비 행사가 조정값: 주가(S)와 행사가(K)의 비율을 로그로 변환 후, 시간(T)과 변동성(σ)으로 보정
        • 위험 중립 세계에서의 기대값: 무위험 이자율(r)과 변동성을 고려한 주가 성장률 반영

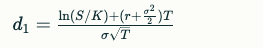
      • d2의 의미

        • d2 = d1 - σ√T
        • 행사 확률: N(d2)는 만기 시 주가가 행사가를 초과할 위험 중립 확률
        • 변동성 감쇠 효과: σ√T 항으로 변동성의 시간에 따른 누적 영향 반영
        • 할인된 행사가 조정: $Ke^{-rT}$와 결합해 미래 가치를 현재가로 환산

      • 계산 예시

        조건 값
        현재가(S) 100,000원
        행사가(K) 110,000원
        변동성(σ) 30%
        무위험율(r) 5%
        기간(T) 1년

      • 계산 과정

      • 해석

        • 55.96% 확률로 주식 보유 시 해지 비율
        • 44.04% 확률로 1년 후 주가가 110,000원 초과

  • 주의할 점

    • 완벽하지 않아요: 실제 장난감 가격은 갑자기 뛸 수 있지만 계산기는 부드러운 변화만 생각해요.
    • 변동성 예측 중요: 날씨 예보처럼 변동성을 잘 맞춰야 정확한 계산이 돼요.

    이 모델은 1973년 피셔 블랙과 마이런 숄즈가 만든 후, 로버트 머튼이 개선했어요. 요즘은 이 계산법을 개량한 몬테카를로 시뮬레이션도 많이 쓰인답니다

Black Scholes 방정식

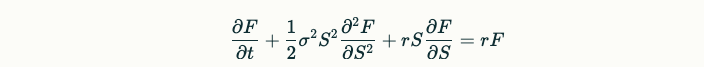
  • 계산 예시

    조건 값
    현재 로봇 가격(S) 10,000원
    약속 가격(K) 11,000원
    변동성(σ) 50% (로봇 가격이 반년에 ±5,000원 변동)
    안전 이자율(r) 10%
    기간(T) 0.5년

  • 공식 적용

  • 계산기 작동 원리

Reference

Share