Course
Regularization
- useful technique for reducing variance.
- There is a little bit of a bias variance tradeoff when you use regularization. It might increase the bias a little bit, although often not too much if you have a huge enough network.
- If you suspect your neural network is over fitting your data, that is, you have a high variance problem, one of the first things you should try is probably regularization. The other way to address high variance is to get more training data that’s also quite reliable. But you can’t always get more training data, or it could be expensive to get more data. But adding regularization will often help to prevent overfitting, or to reduce variance in your network.
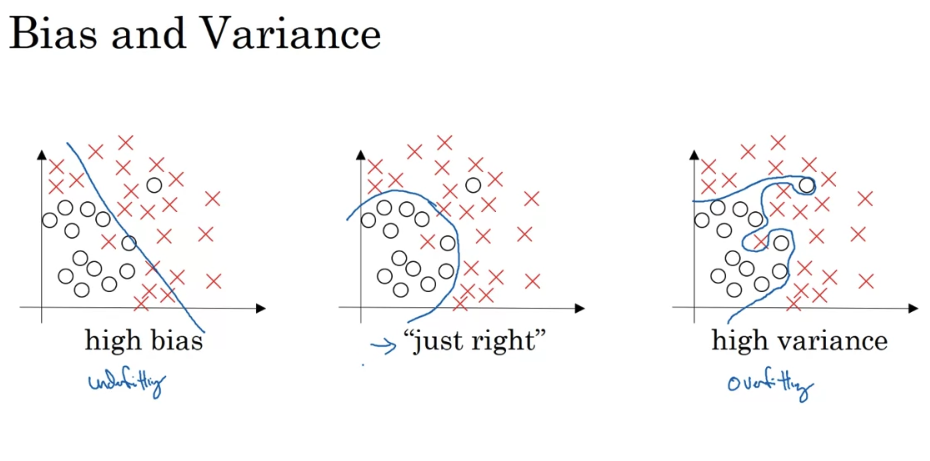
Why does regularization help with overfitting? Why does it help with reducing variance problems?

- Simplicity and Generalization: Regularization encourages the model to be simpler by penalizing large weights. Simpler models tend to generalize better to new data because they are less likely to fit to the noise in the training data. This is achieved by adding a penalty term to the loss function that is proportional to the magnitude of the weights (parameters). This penalty term could be the L1 norm (sum of absolute values of weights) or L2 norm (sum of squares of weights) of the model parameters. The L1 norm leads to Lasso regularization and the L2 norm leads to Ridge regularization.
- Reducing Model Complexity: By penalizing large weights, regularization effectively reduces the model’s complexity by discouraging learning a highly flexible model, which would lead to overfitting. In this way, it helps in reducing the variance of the model. High variance is a sign of overfitting where the model is too sensitive to the small fluctuations in the training set and hence may not perform well on the unseen data.
- Feature Selection (for L1 regularization): In the case of L1 regularization, it can shrink some of the weights to zero, effectively performing feature selection. This means the model becomes simpler and more interpretable, and can improve generalization by reducing overfitting to irrelevant features.
Dropout Regularization
- the thing to remember is that drop out is a regularization technique, it helps prevent overfitting. And so unless my avram is overfitting, I wouldn’t actually bother to use drop out. So as you somewhat less often in other application areas, there’s just a computer vision, you usually just don’t have enough data so you almost always overfitting, which is why they tend to be some computer vision researchers swear by drop out by the intuition.
- One big downside of drop out is that the cost function J is no longer well defined on every iteration. You’re randomly, calling off a bunch of notes.
Other Regularization: Data Augmentation, Early Stopping
Normalizing Inputs: If your input features came from very different scales, maybe some features are from 0-1, sum from 1-1000, then it’s important to normalize your features. If your features came in on similar scales, then this step is less important although performing this type of normalization pretty much never does any harm.
Gradient Checking Implementation Notes

Optimization
exponentially weighted averages
bias correction
Adam Optimization Algorithm

- Adam: Adaptive moment estimation
- Beta_1 is computing the mean of the derivatives. This is called the first moment
- Beta_2 is used to compute exponentially weighted average of the squares, and that’s called the second moment.
Local Optima
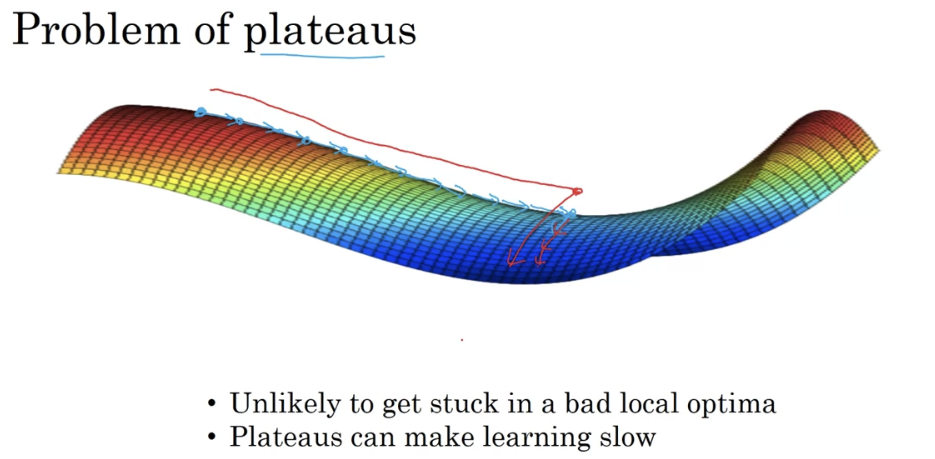
- first, you’re actually pretty unlikely to get stuck in bad local optima so long as you’re training a reasonably large neural network, save a lot of parameters, and the cost function J is defined over a relatively high dimensional space.
- But second, that plateaus are a problem and you can actually make learning pretty slow. And this is where algorithms like momentum or RmsProp or Adam can really help your learning algorithm as well. And these are scenarios where more sophisticated observation algorithms, such as Adam, can actually speed up the rate at which you could move down the plateau and then get off the plateau.
Hyperparameter

- Batch norm means that, especially from the perspective of one of the later layers of the neural network, the earlier layers don’t get to shift around as much, because they’re constrained to have the same mean and variance. And so this makes the job of learning on the later layers easier. It turns out batch norm has a second effect, it has a slight regularization effect. So one non-intuitive thing of a batch norm is that each mini-batch, I will say mini-batch X_t, has the values Z_t, has the values Z_l, scaled by the mean and variance computed on just that one mini-batch.