자기 상관 함수와 부분 자기 상관 함수
Autocorrelation Function, 자기 상관 함수
자기 상관 함수(Auto-correlation Function)
- 어떤 신호의 시간이동 된 자기 자신과의 ‘상관성(Correlation)’ 척도
- 주요 특징
- 결정 신호(주기 신호/비주기 신호)이든, 랜덤 신호 이든 모든 신호에 대해 적용 가능
- 특히 랜덤 과정인 경우에
- 자기상관함수를 이용하여 굳이 시간신호에 대한 푸리에 변환을 구할 필요 없이
- 주파수상에 분포된 전력(전력밀도스펙트럼)을 취급할 수 있으므로 이를 사용하게 됨
- [참고]
- 서로 다른 신호 간의 상관성 척도에 대해서는 상호상관 참조
- 상관데 대한 보다 정확한 이해를 위해서는 상관성 참조
- 상관성 개념의 종합화/일반화는 비교(같음/닮음/다름) 참조
확정적 신호(Deterministic signal)에서, 자기 상관 함수
- 에너지신호의 자기상관함수: 컨볼루션(*)에 의해 정의돔
- x(t)가 실수 신호이면, $Rx(τ)=∫^∞ _{−∞} x(t)x(t+τ)dt=x(τ)∗x(−τ)$
- x(t)가 복소수 신호이면, $Rx(τ)=∫^∞_{−∞}x(t)x^∗(t+τ)dt=x(τ)∗x^∗(−τ)$
- 전력신호의 자기 상관 함수: 시간평균(<>)에 의해 정의됨
실수 신호
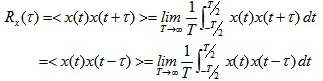
복소수 신호
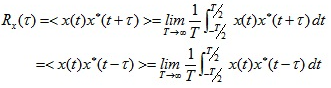
- 에너지신호의 자기상관함수: 컨볼루션(*)에 의해 정의돔
랜덤 과정(Random Prodcess)에서, 자기상관 함수
- 정의
- 통계적 평균에 의한 자기상관함수 정의: $R_x(t_1,t_2) = E[X(t_1)X(t_2)]$
- 결합 PDF(결합 확률밀도함수)에 의한 자기 상관함수 정의: $R_x(t_1,t_2) = ∫^∞_{−∞}∫^∞_{−∞}x_1x_2fx_1x_2(x_1,t_1,x_2,t_2)dx_1dx_2$
- 만일 랜덤 과정이 광의의 정상과정이면,
시간 t의 함수가 아니라 시간천이 $t-t=τ$의 함수가 됨
$R_x(t_1,t_2) = R_x(t,t+τ)=R_x(τ) = E[X(t)X(t+τ)]$
이때 시간 영역 자기상관과 주파수영역 스펙트럼밀도 간에 푸리에 변환 쌍 관계가 있음.
$R(τ)$ ← 푸리에변환 쌍 관계 → $S(f)$
만일, 랜덤과정이 에르고딕과정이라면,
통계적 평균 및 시간 평균이 상호 호환이 가능함
$R_x(τ) = E[X(t)X(t+τ)] =< X(t)X(t+τ)>$
따라서 이 경우에는 R(τ)는 시간 평균이나 통계적 평균 어느 것으로도 구할 수 있음.
- 정의
자기상관 함수의 성질/특징
신호의 ‘시변(time-variant)’ 특성이 어떤가를 보여줌
그 신호가 갖는 스펙트럼의 특성 정보를 나타냄
시간적인(시변) 상관성 척도임
- 분산이 확률변수가 통계적으로 불규칙하게 분포되는 정도를 나타내는 척도라면 자기 상관은 분산과 유사하게 확률과정이 시간적으로 상관 또는 분산되는 척도를 나타냄
직관적으로 자기 자신과의 시간천이(τ)가 작을수록 상관성이 커짐
따라서 τ = 0 에서 최대 상관성 값을 갖음
$|R_x(τ)|≤R_x(0)$식
τ = 0 일때 물리적 의미로는
에너지 신호: τ = 0 에서의 최대값이 전체 신호에너지와 같음
$R_x(0) = ∫^∞_{−∞}|x(t)|^2dt= E_x$
전력신호: τ = 0 에서의 최대값이 평균 전력과 같음
$R_x(0) =< x^2(t) >= ∫^∞_{−∞}S_x(f)df = P_{av}$
WSS 랜덤과정: τ = 0에서의 최대값이 평균전력과 같음
$R_x(0) = E[X^2(t)] = ∫^∞_{−∞}S_x(f)df = P_{av}$
시간 영역 자기 상관과 주파수 영역 스펙트럼 밀도 간에 푸리에 변환 쌍 관계가 있음
- 자기 상관 ← 푸리에변환 쌍 관계 → 스펙트럼 밀도 : 위너킨친정리 참조
Partial Autocorrelation Function, 부분 자기 상관 함수
- 편 자기 상관 함수(부분자기상관함수)는 다른 모든 짧은 시차 항에 따라 조정한 후 k 시간 단위로 구분된 시계열($y_{t-1},y_{t-2},…,y_{t-k-1}$)의 관측치 ($y_t 및 y_{t-k}$) 간의 상관의 측도임
- 해석
ARIMA 모형에서 자기 회귀 차수를 식별하는 용도로 사용 됨.
편 자기 상관 함수에서 다음과 같은 패턴을 찾음.
각 시차에서 큰 값을 조사하여 유의한지 확인함.
유의한 큰 값은 유의 한계를 벗어나면, 이는 해당 시차에 대한 상관이 0이 아니라는 것을 나타냄

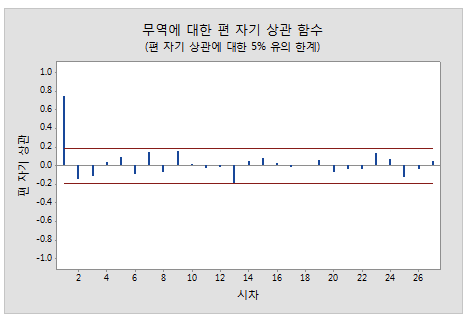
- 이 그림에서는 시차 1에 유의한 상관이 있고 그 뒤에는 유의하지 않은 상관이 있음.
- 이 패턴은 1차 자기회귀 항을 나타냄.