Data AnalysisModel

Support Vector Machine

1. 분류에 대한 수적 표현

  • 학습 데이터 X(독립변수),Y(종속변수)가 있을 때 (i=1,2,3,4,5 ….데이터의 갯수) Y⇒{-1,1} (두 개의 클래스를 의미)

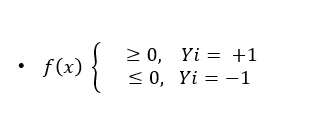
⇒ 경우에 따라서, 클래스를 1과 -1 로 나눔

Y(정답) * F(x)(예측한 정답) >0 라는 것은 제대로 분류된 형태 ( 같은 부호끼리 곱하면 양수인 경우니까)

2. 선형 분할(Linear Classifier)

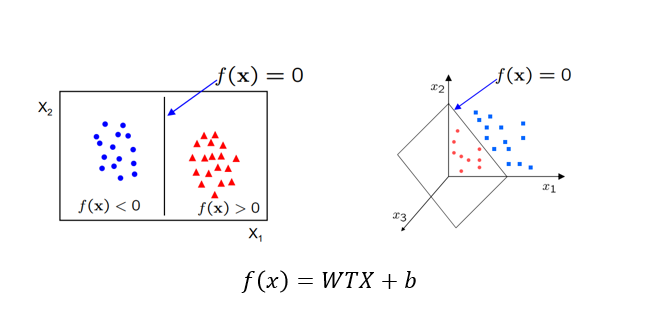
  • f(x)= W transpose X + b (선형조합, 각각의 항들이 더하기로 이루어진 조합.)
  • 선형분할은 직선으로 나누는 것 (2차원이건 3차원이건 그 이상이건 상관 없음)
  • b(bias) Y 절편을 의미
  • W는 직선의 기울기

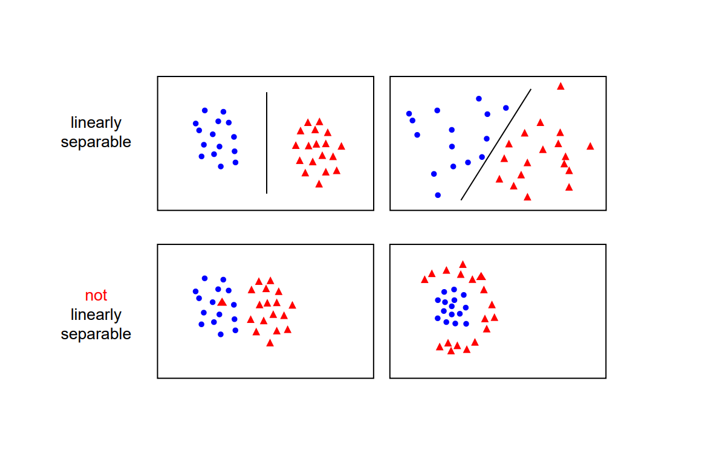
3. 초평면 분할

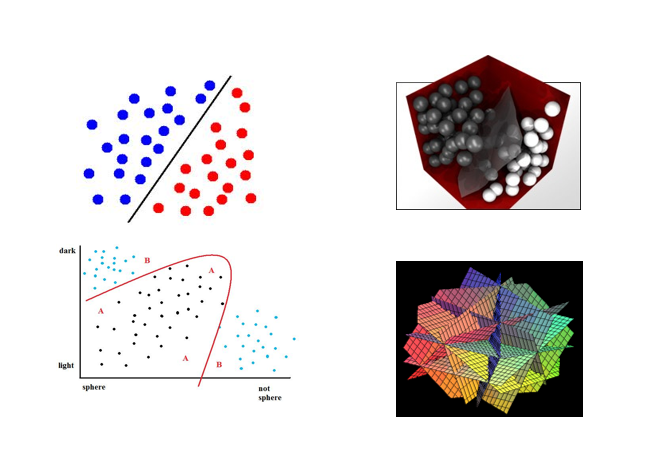
더 나은(최적) 분류를 위한 초평면(Hyperplane)→선 보다 더 큰 차원

좋은 판별선에 대한 기준

  • 최적화: 좋은 것 을 극대화 시키고 나쁜 것 을 극소화 시키는 것
  • 분류에서의 최적화: 잘 안나뉘는것 , 잘 나뉘는 것

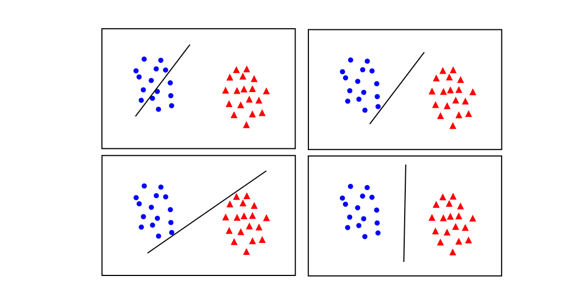
  • 나중에 Testing data 를 돌렸을때, 가장 좋게 나뉜 것은 반절로 나뉜 직선이다. Test data 가 어떻게 들어올지 모르는 것 이기때문에 , 과적합 되어 있는 것보다 확실히 절반으로 나누는것이 좋다.

최적의 분할 초평면 찾기

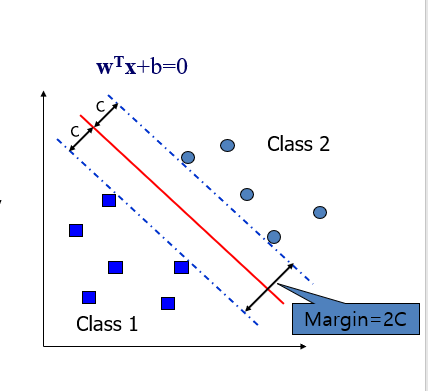
  • Margin: c는 선형분할의 각 클래스별 거리 각 클래스별 거리를 합친 것
  • Margin=2c를 최대화 하는, w T x +b=0 의 직선을 찾아야 하는것 이다.
  • Marign 을 최대화 시키는 초평면이 최적
  • “Learning Theory” 에 따르면, Marigin을 최대화 시키는 초평면이 일반화 오류가 가장 낮게 나타남(Test data 에서도 좋은 점수가 나온다)
  • Margin:초평면과 가장 근접한 각 클래스 관측치와의 거리의 합.

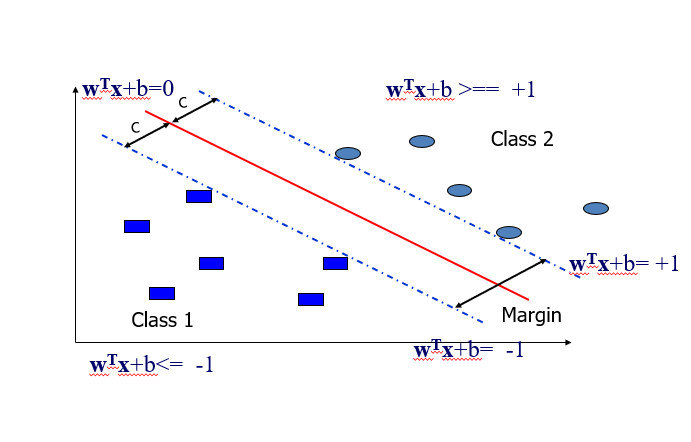
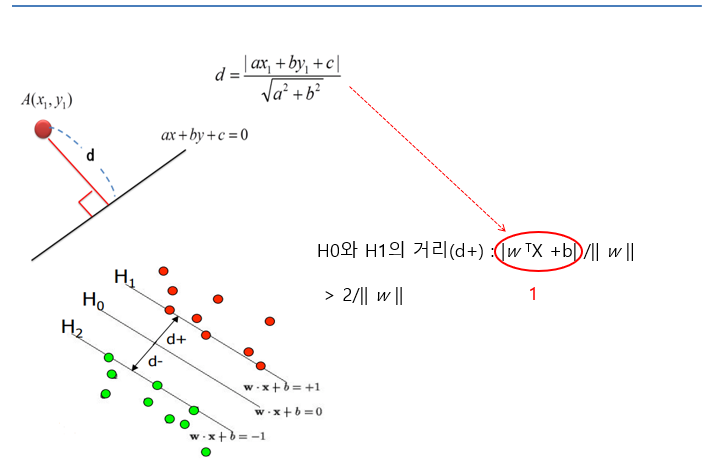
Margin 수식 유도

  1. 일반적인 방법

  1. 점과 선 사이의 거리
    • 거리 d 가 2개이니까 2/||W||

Margin 최대화 (최적화)

  • ||w|| 가 분모에 있기 때문에 결국 ||w|| 를 최소화 해주는것 이 2/||w|| 를 최대화 해주는거랑 같다고 할 수 있다
  • 우리는 결국 w 값을 최소화 시켜주는것이 목적이기 때문에 제곱을 취해주든 상수를 곱해주는 상관이 없다

  • Lagrange Multiplier(수학적 기법) ⇒ 제약조건을 최적화 조건에 녹여버리는 기법.

  • Xi tranpose X ( 학습데이터와 분류할 데이터의 내적)

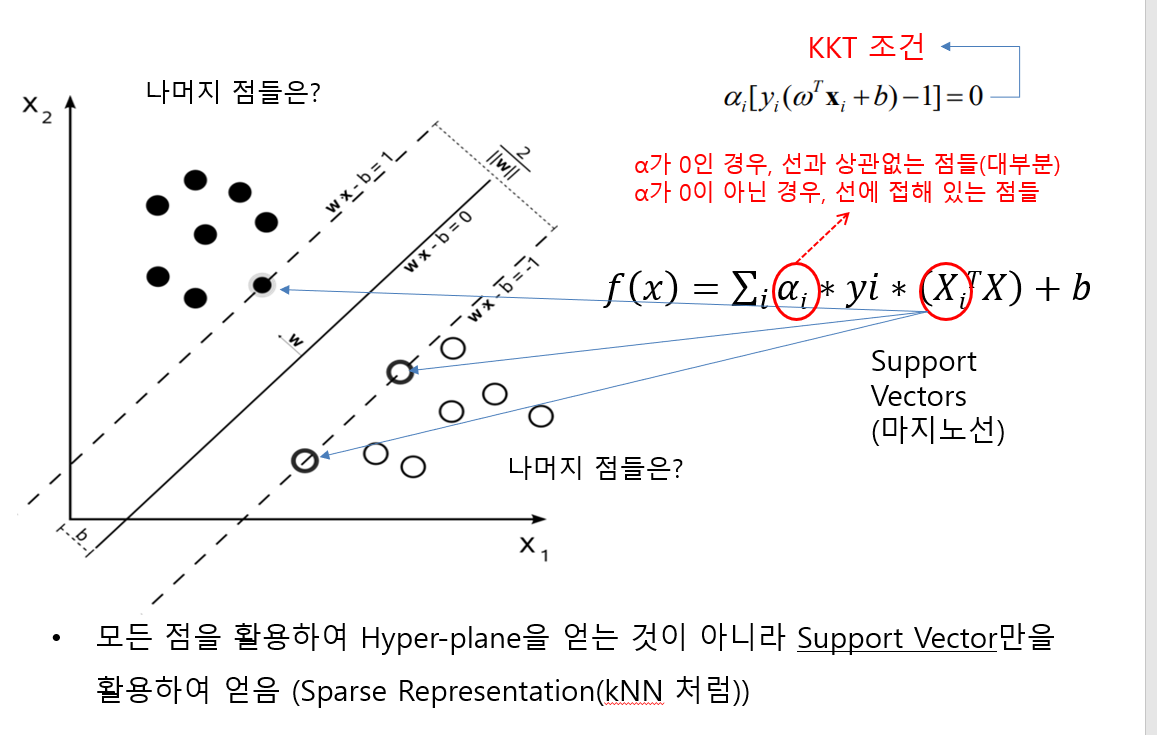
4. SVM(Support Vector Machine)

  • 판별식에 서포트벡터만 사용하기 때문에 아웃라이어에 대한 영향을 안 받음(KKT 조건으로 걸러냄)
  • KNN 또한 이웃을 확인하는 개수인 K의 한계가 있어서 어느 elbow point 를 지나치면 정확도가 떨어진다. → 비슷한 원리 ⇒ svm 또한 분류를 유효하게 하기위해서 support verctor 만 이용해준다.

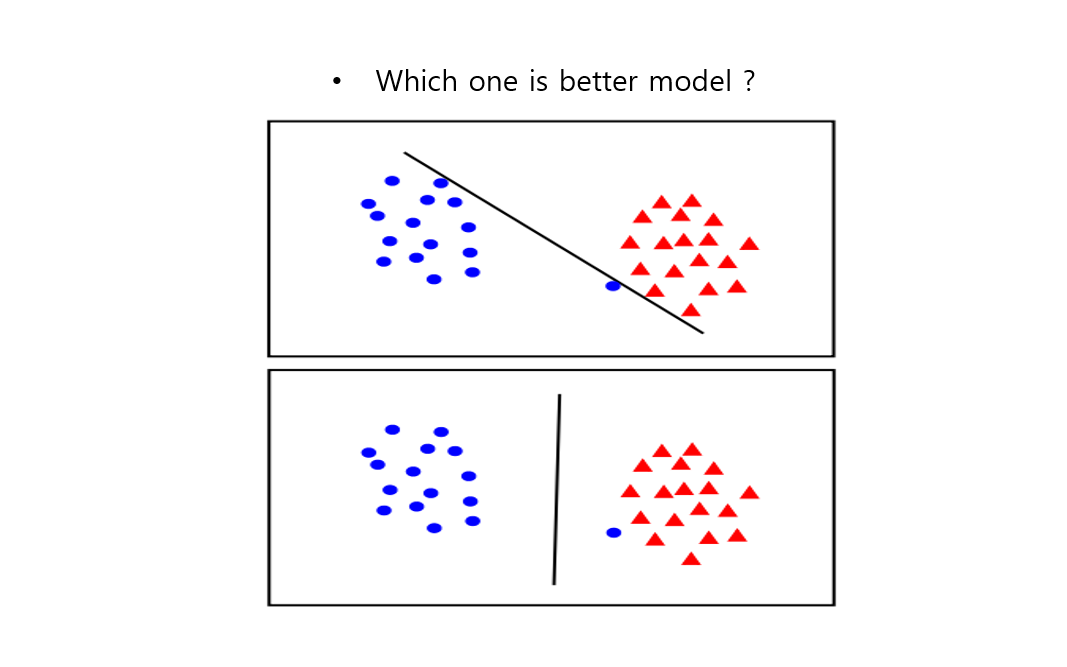
  • 선형으로 완벽히 나눠지지 않는 데이터라면 테스트 데이터에게는 위의 모델 보다 아래 모델이 더 좋을 것 으로 보인다. 하지만 SVM 의 제약조건에는 트레인데이터가 완벽하게 나누어져야 한다는 제약 조건이 걸려있다. 어떻게 하면 좋을까?

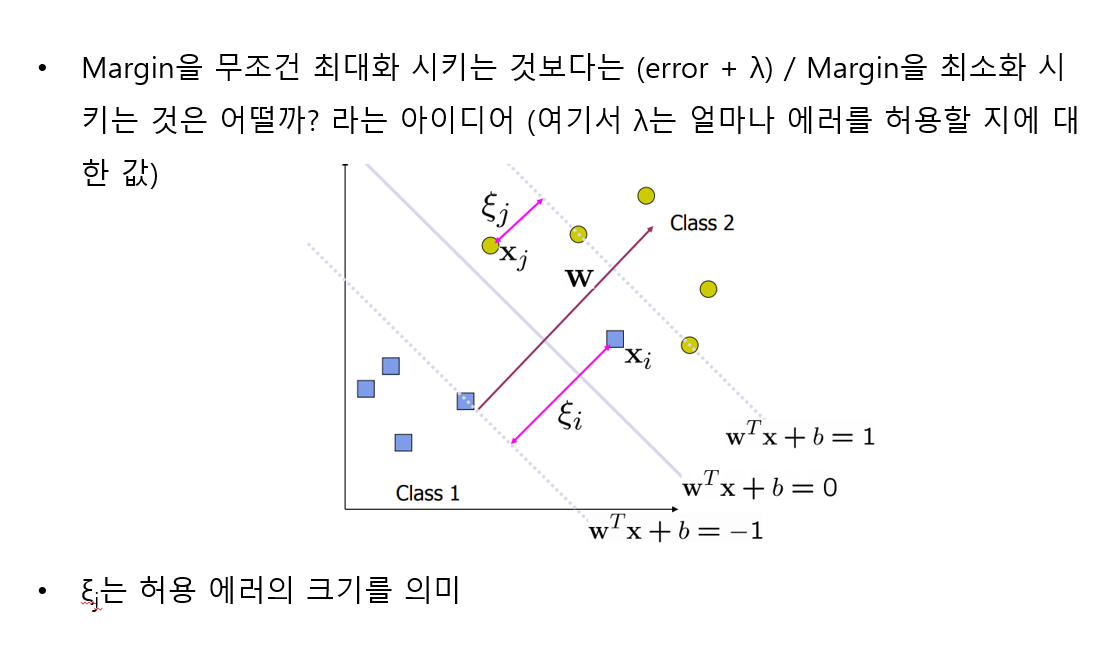
Slack Variable for “Soft Margin”

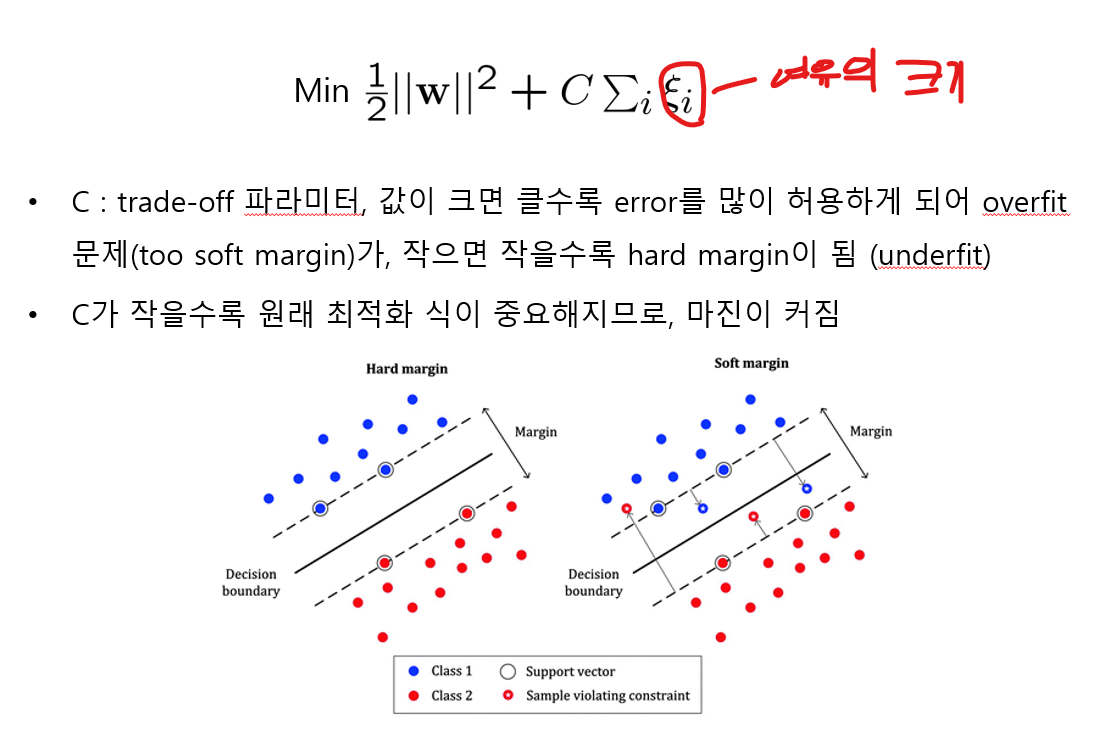
Soft Margin SVM

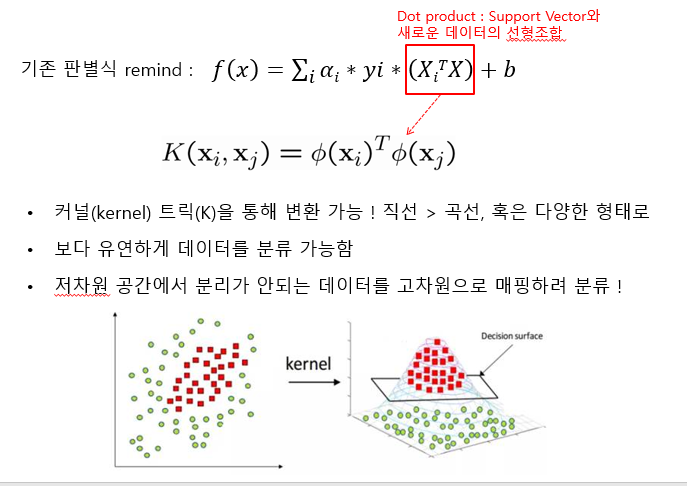
Non-linear SVM

  • Reference: 한국공학대학교 경영학과 강지훈 교수님 강의
Share