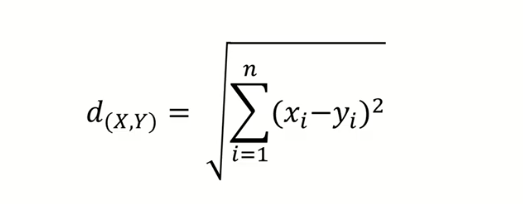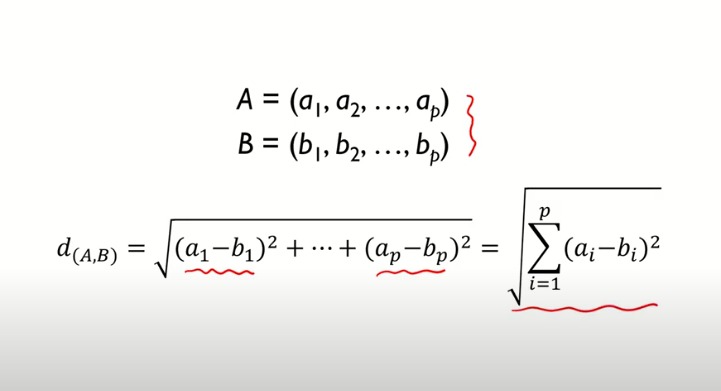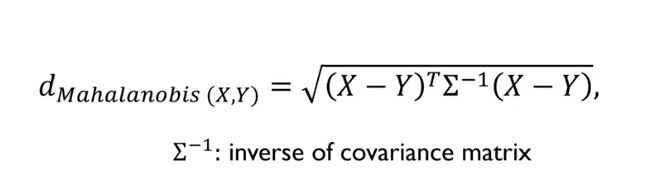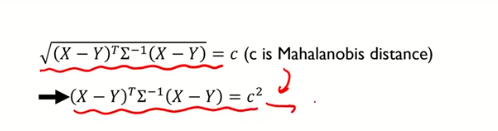1. Euclidean distance
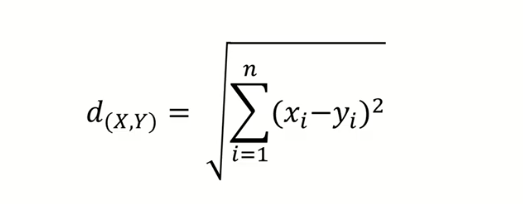
- 가장 흔히 사용하는 거리측도
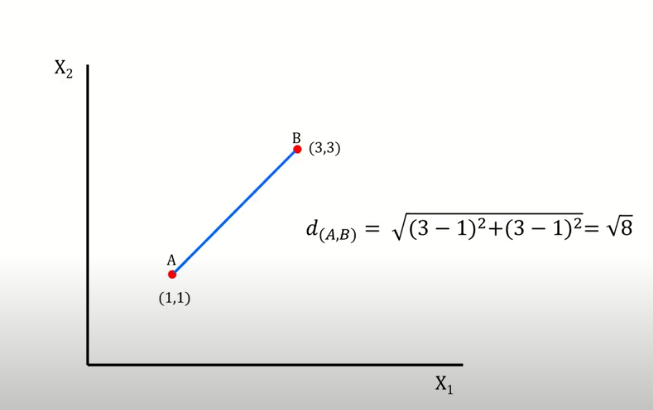
- 대응되는 x,y값 간 차이 제곱합의 제곱근으로써, 두 관측치 사이의 직선 거리를 의미함.
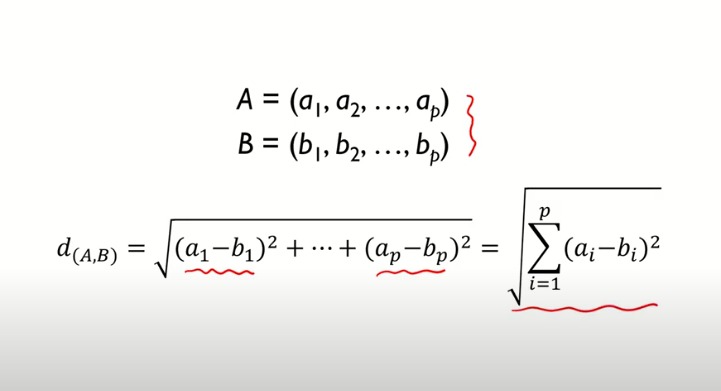
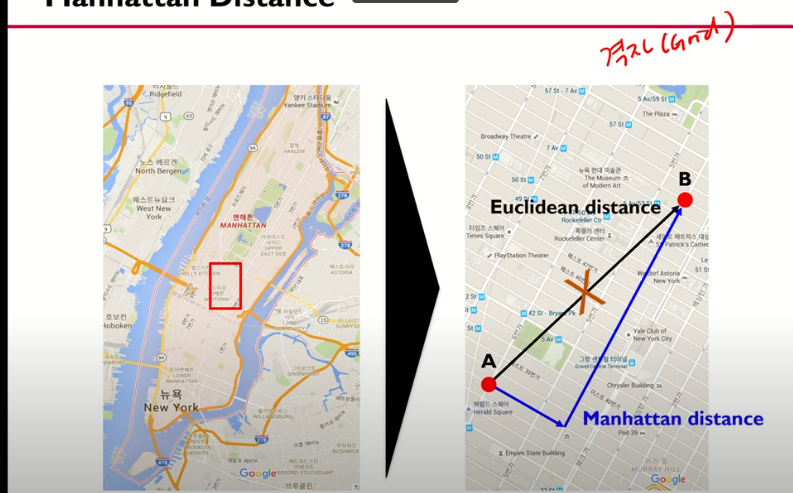
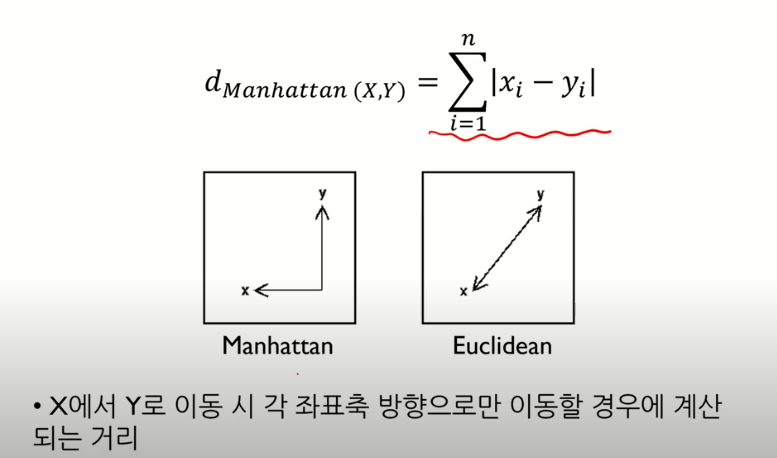
2. Manhattan Distance
- 맨하탄은 블럭이 나누어져 있어 직선으로 갈 수가 없다.
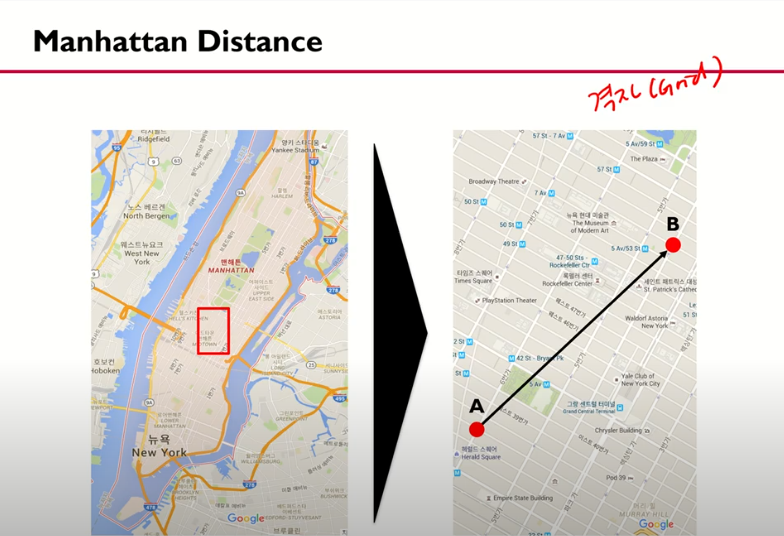
- 직선거리가 아닌 격자거리.
- 격자:바둑판처럼 가로세로를 일정한 간격으로 직각이 되게 짠 구조나 물건.
3. Mahalanobis Distance
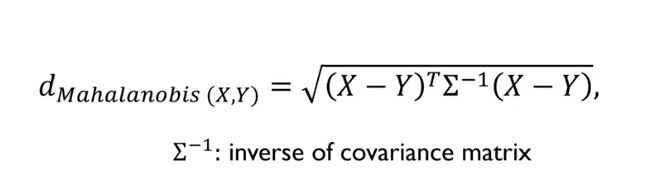
- 변수 내 분산,변수 간 공분산을 모두 반영하여 x,y,간 거리를 계산하는 방식⇒변수간 상관관계를 고려한 거리지표이다.
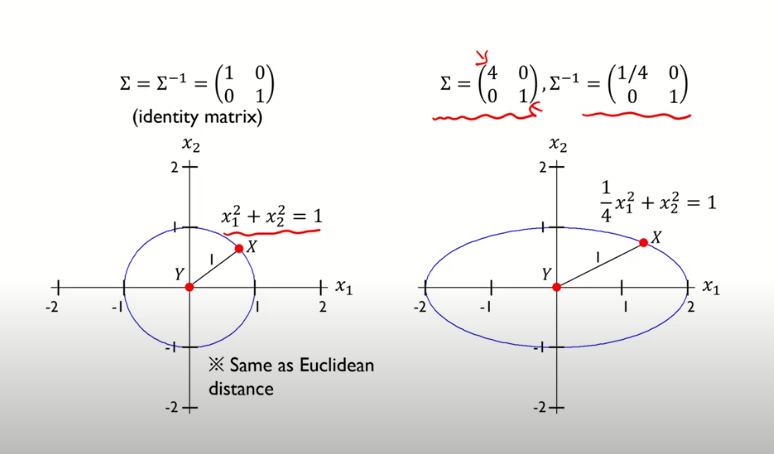
- 데이터의 공분산 행렬이 단위행렬인 경우는 유클리디안 거리와 동일함
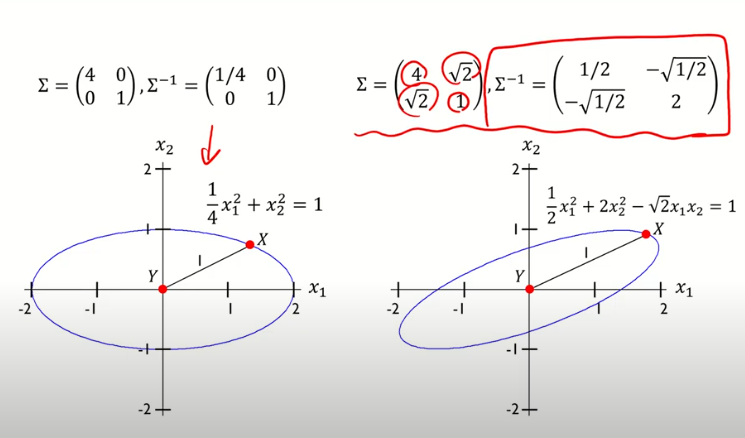
- 공분산 행렬의 역행렬을 취했다는 것 → 분산이 분모에 들어간다는 뜻 → 분산이 커지면 거리가 작아지고 , 분산이 작아지면 거리가 길어짐
- 마할라노비스거리가 제곱근이 취해져 있기 때문에 제곱근을 없앴다.
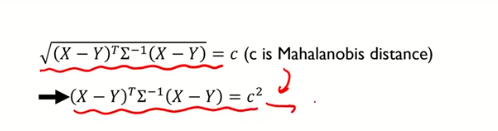
- 2차원 행렬로 비유를 했을시 , 쭈욱 대입하면 아래의 식으로 나타난다

- y값에 0,0 을주고 대입하면 타원의 방정식이 나온다.

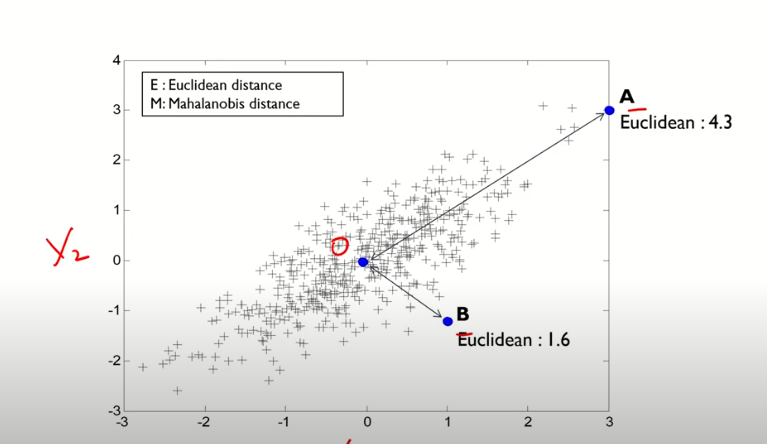
- 유클리디안 관점에서는 중앙점과 비교했을때, A가 더 멀다.
- 상관관계를 고려한 마할라노비스 거리로 보면 B가 더 멀다
- Reference: 한국공학대학교 강지훈교수님 강의